Amortization Deep Dive: The Rule of 78s
As we talked about previously, there are many reasons why understanding amortization methods is helpful for financial professionals. Today, we’re...
4 min read
 Cindy Fisher
:
June 25, 2020
Cindy Fisher
:
June 25, 2020

I remember being in Mr. Harrison’s 6th grade math class when he described interest to us. He said that if we had a 30-year mortgage and took all 30 years to pay off the loan, the real cost of the house would be triple what we paid for it. That was the day that sparked my interest in … interest.
Calculating interest may sound boring to some, but to financial professionals, it may be one of the most fascinating parts of the job.
GOLDPoint Systems has five different ways to calculate interest.
This blog post will attempt to help you understand the different calculation methods just a little better. They’re very well known in the financial industry, but sometimes it helps to have it explained in a way that makes it click. The Interest Calculation Method field is one of the most important fields in our whole system.
Technically, GPS has 10 different Interest Calculation Methods, but five of them use the same calculation formula as the first five while allowing the Date Interest Paid to and Date Last Accrued to be more than one frequency behind the Due Date (whereas the first five calculation methods do not allow that). There are some other slight variations with the other five Interest Calculation Methods based on payment frequency (monthly, bi-weekly, etc.). We’ll discuss those in another blog post.
For this post, let’s focus on the following Interest Calculation Methods:
Code 1 – 365/365 days per year
If the Interest Calculation Method is set to “1 – 365/365”, monthly interest for the P/I Constant is calculated as follows:
Principal Balance amount as of last payment X Interest Rate ÷ 365 X days difference from last Due Date to current Due Date = the amount of payment that goes towards interest. The rest of the P/I Constant, after paying interest, goes to principal.
Example:
P/I Constant is $200.
Principal Balance as of last payment date = $25,000
Interest Rate = 5.75%
Last Due Date to this Due Date = 31 days
Interest Calculation Method = 1 – 365/365
Interest calculation:
25,000 X .0575 ÷ 365 X 31 = $122.09 ← This is the amount of interest paid from the P/I Constant.
200.00 – 122.09 = $77.91 ← This is the amount applied to principal from the P/I Constant.
Code 2 – 360/360 days per year
Code 2 considers every month as having 30 days. February and all the months with 31 days are considered 30-day months.
Principal Balance X Interest Rate ÷ 360 X 30 = Interest amount of payment
Example:
P/I Constant is $200.
Principal Balance as of last payment date = $25,000
Due Date to Due Date = 31 (but the calculation will use 30)
Interest Rate = 5.75%
Interest calculation:
25,000 X .0575 ÷ 360 X 30 = $119.79 ← This is the amount of interest paid from the P/I Constant.
200.00 – 119.79 = $80.21 ← This is the amount applied to principal from the P/I Constant.
Code 3 – 365/360 days per year
When using Code 3, the annual interest rate is divided by 360 to get the daily interest rate, and then multiplied by the number of days from last Due Date to current Due Date.
Principal Balance X Interest Rate ÷ 360 X days difference from last Due Date to current Due Date = Interest amount
Example:
P/I Constant is $200.
Principal Balance as of last payment date = $25,000
Interest Rate = 5.75%
Due Date to current Due Date = 31 days
Interest calculation:
25,000 X .0575 ÷ 360 X 31 = 123.78 ← This is the amount of interest paid from the P/I Constant.
200.00 – 123.78 = $76.22 ← This is the amount applied to principal from the P/I Constant.
Code 4 – 360/365 days per year
Simply put, Code 4 is like a 365-day simple daily calculation (Code 1) but looks like a 360-day calculation (Code 2) where each month has 30 days. Like Code 1, this method calculates interest accruals every day using a daily per diem interest amount.
Principal Balance X Interest Rate ÷ 365 X 30 (because every month is considered 30 days) = Interest
Example:
P/I Constant is $200.
Principal Balance as of last payment date = $25,000
Interest Rate = 5.75%
Every month is considered 30 days of interest (even though Due Date to Due Date is 31)
Interest calculation:
25,000 X .0575 ÷ 365 X 30 = 118.15 ← This is the amount of interest paid from the P/I Constant.
200.00 – 118.15 = $81.85 ← This is the amount applied to principal from the P/I Constant.
Code 5 – 366/366 days in a leap year
Code 5 is like a 365-day simple daily calculation (Code 1) but it also considers leap years. So, when there is a leap year, it calculates using 366, and when there isn’t a leap year, it calculates using 365.
Principal Balance X Interest Rate ÷ 366 (if leap year/365 if non-leap year) X number of days from Due Date to Due Date = Interest
Example:
P/I Constant is $200.
Principal Balance as of last payment date = $25,000
Interest Rate = 5.75%
Last Due Date is 02/15/2020 and next Due Date is 03/15/2020 (a leap year) = 29 days
Interest calculation:
25,000 X .0575 ÷ 366 X 29 = 113.90 ← This is the amount of interest paid from the P/I Constant.
200.00 – 113.90 = $86.10 ← This is the amount applied to principal from the P/I Constant.
Here’s a cool little trick that will bring home the differences in interest calculation in a more illustrious way.
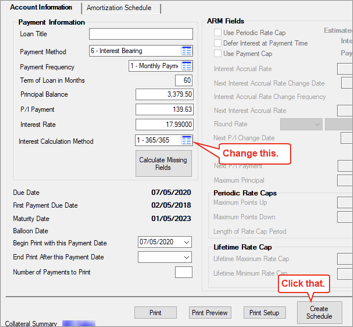
-Jun-25-2020-04-16-45-13-PM.png)

As we talked about previously, there are many reasons why understanding amortization methods is helpful for financial professionals. Today, we’re...

In today's digital age, where online banking and electronic communication have become the norm, ensuring the security of financial information is...

If you spend any amount of time looking over GOLDPoint Systems documentation, you’ve probably come across the term GILA Loan once or twice. But what...

Loans can be categorized with one payment method. Our system allows seven possible payment method codes. Payment method codes determine how interest...

GOLDPoint Systems categorizes loans once they’ve been opened into seven different payment methods. The payment method determines how to calculate...

Precomputed interest loans are a popular method of lending for borrowers requesting less than a few thousand dollars for a loan term of less than...